Hacks

Digitally Programmable Analog Computer (DPAC)

In Spring 2019, Kaustubh Porlikar, Deepak Gopalan and I built a hybrid analog-digital computer for our Electronics Design Lab course at IIT Bombay. Many sleepless nights were involved.

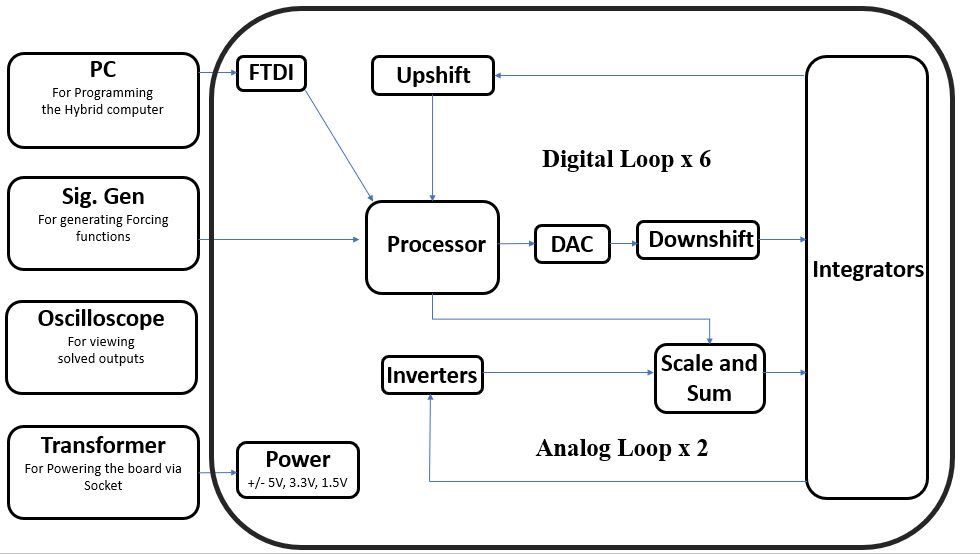
The problem: Engineers often test controllers using simulated environments (hardware-in-the-loop). These simulations involve solving differential equations, which digital computers do iteratively—and slowly.

Our solution: Use analog circuits for the heavy lifting (integration via op-amps is instant), while a digital processor handles the tricky nonlinear parts. Best of both worlds.

DPAC v2.0 can solve systems up to 8th order, handling equations of the form:

• x' = Ax + bu + f(x,u)
• y = Cx + du + g(x,u)

where f and g are nonlinear functions.

The board is self-contained with onboard power management and can be programmed via its microcontroller. We also built DPAC β2.0, a smaller 2-variable version with programmable switches that let it adapt to different frequency ranges on the fly.

Full technical report here. Thanks to Prof. Mukul Chandorkar for encouraging this madness.

Lower Bounds for Simple Policy Iteration (Cracking a 30-year-old puzzle)

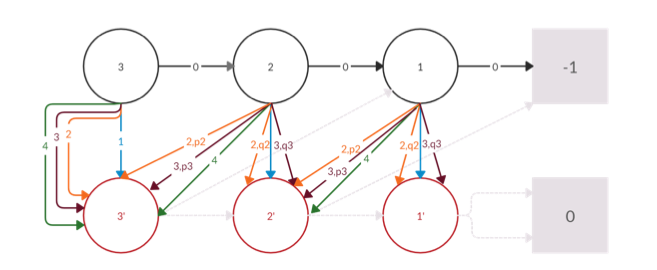
Context: Markov Decision Processes (MDPs) model sequential decision-making—think robots, games, or any agent choosing actions over time. An MDP has states, actions, rewards, and a discount factor.

Policy Iteration finds the optimal strategy by alternating two steps:

• Evaluate: How good is the current policy?
• Improve: Switch to better actions where possible.

The question: How many iterations does this take? In 1990, Melekopoglou and Condon proved lower bounds for "Simple Policy Iteration" (a specific variant), but only for 2 actions.

Our contribution: In late 2019, we extended this to multiple actions. We designed a new class of MDPs and proved non-trivial lower bounds, reopening a puzzle that had been dormant for 30 years. Paper here.